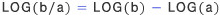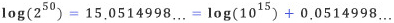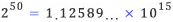[mathematics] 상용로그 - 로그의 발견

로그표는 작은 표이지만 이를 이용하면, 대단히 쉬운 계산을 통해 공간에서의 모든 기하학적 크기와 운동에 대한 지식을 얻을 수 있다. 이 표는 작다고 불려 마땅한데, 사인(sine) 표의 크기를 넘지 않기 때문이다. 대단히 쉽다고 불려 마땅한 것은, 이 표를 통하면 모든 곱셈, 나눗셈 및 훨씬 어려운 제곱근 구하기를 피할 수 있기 때문인데, 대단히 적고도 무척 간단한 덧셈, 뺄셈, 2로 나누기를 통해 상당히 일반적으로 모든 도형과 운동의 치수를 셈할 수 있다.’

 

다소 자신에 찬 위의 글은 존 네이피어(John Napier, 1550-1617)의 사후 1619년에 발표된 저작 ‘놀라운 로그법의 구성’(Mirifici logarithmorum canonis description)의 서문 첫머리이다. 자신이 발명한 로그표를 이용하면, 곱셈, 나눗셈, 제곱근 등을 덧셈, 뺄셈, 2로 나누기만을 통해 쉽게 계산할 수 있다고 선언한 것이다. 네이피어가 말하는 로그 가 무엇인지 설명하려 하는데, 이에 앞서 네이피어 이전 시대에는 과연 어떻게 계산을 했는지 살펴 보는 것이 순서일 것 같다.

 

삼각함수로 곱셈을 쉽게 하기

덧셈이나, 뺄셈 등의 연산은 비교적 계산이 쉬운 편에 속한다. 하지만 두 수를 곱하거나 나누는 것은 생각보다 계산이 많이 필요한데, 옛날 사람들은 어떻게 계산한 것일까? 그냥 곱했을까? 놀랍게도 아니다. 16 세기 후반에는 삼각함수를 이용한 방법이 풍미했다. 비티히(Paul Wittich, 1546-1586)와 클라비우스(Christopher Clavius, 1538-1612) 등이 개발한 것으로 알려진 이 방법은 아래와 같은 삼각함수의 덧셈 정리를 이용한다.

 

 

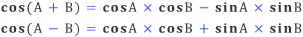
두 식을 더한 뒤에 반으로 나누면 다음 사실을 알 수 있다.

 

 

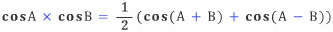
이 식과 코사인 함수표를 이용하면 (실제로는 사인 함수표도 이용했지만, 설명의 편의를 위해 코사인을 사용한다), 곱셈을 비교적 쉽게 할 수 있다. 예를 들어, a=57.36과, b=292.4를 곱하려면, 0.5736, 0.2924를 곱한 뒤, 10만을 곱해주면 된다. 따라서 1보다 작은 두 수의 곱만 알면 족하다. 편의상 양수만 생각하기로 하는데, 1보다 작은 수는 항상 어떤 수의 코사인 값이다. 실제로 삼각함수표를 뒤적여보면 다음과 같다.

 

 

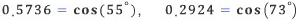
위의 공식에 대입하면, 아래와 같이 된다.

 

 

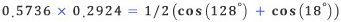
다시 삼각함수표를 훑어보면, cos(128°) = -cos(52°) = -0.6157, cos(18°) = 0.9511이므로 아래와 같은 결과를 얻을 수 있다.

 

 

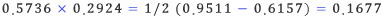
실제로 두 수를 직접 곱해보면 0.16772064이므로 오차가 있는데, 이는 0.5736과 0.2924가 cos(55°)와 cos(73°)의 참값이 아니라, 소수점 이하 네 자리까지만 구한 근삿값이기 때문이다. 더 정확한 삼각함수표를 쓴다면 당연히 계산값도 훨씬 정밀해지는데, 연습 삼아 몇 번만 계산해 보면 누구나 무릎을 치며 탄복할 계산법이다. 나눗셈의 경우 시컨트와 코시컨트 함수를 이용해서 계산했고, 제곱근은 삼각함수의 반각공식을 이용해서 비슷하게 계산할 수 있는데, 굳이 설명할 필요는 없을 것 같다.

 

오늘날처럼 계산기가 발달한 세상에 사는 우리로서는 저렇게까지 하고 싶었을까 고개를 갸우뚱할 수도 있겠는데, 개구리가 올챙이적 생각을 못하는 것과 별반 다르지 않다. 더구나 십진 기수법이나 소수점 표기법마저도 정착되지 않았던 시절에 큰 수를 곱하는 것은 사실상 악몽이었다는 것을 기억해 둘 필요가 있다. 천문학적 숫자를 다뤄야만 했던 천문학자들에게는 이런 계산이 일상다반사였으므로 정밀한 삼각함수표는 필수였다.

 

네이피어의 로그

16세기 후반 최고의 천문학자 티코 브라헤(Tycho Brahe, 1546-1601)는 삼각함수를 이용한 빠른 곱셈법에 능통했다. 브라헤는 덴마크로 가다가 날씨 때문에 자신의 천문대를 방문한 왕자(훗날 영국의 왕 제임스 1세가 된다)에게 이런 계산법을 시범 보였다고 한다. 당시 주치의로 동행했던 존 크레이그(John Craig, ??-1620)는 이 계산법을 절친한 친구 존 네이피어에게 보여준다. 이에 자극을 받은 네이피어는 20여 년간 연구를 거쳐 ‘로그’(logarithm)를 발견하고 1614년 ‘로그의 놀라운 규칙’(Mirifici logarithmorum canonis description)를 통해 발표한다. 로그의 규칙이 왜 놀랍다는 것인지 이제부터 살펴보겠는데, 현대적으로 각색하여 표현하기로 한다.

 

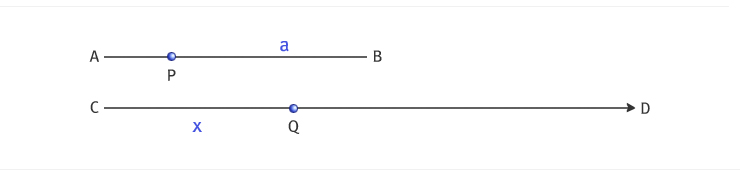
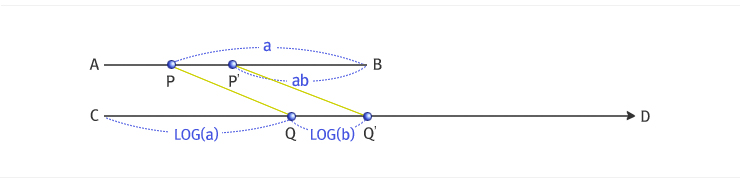
길이가 일정한 선분 AB와 무한반직선 CD가 있다고 하자. 네이피어는 선분 AB의 길이를 10⁷이라고 했지만 우리는 편의상 1이라고 해보자. 이제, A, C에서  각각 점 P, Q가 동시에 속도 1로 출발하여 움직인다. 단 P의 속도는 PB 의 길이 a와 같도록 줄어들고, Q의 속도는 항상 1로 일정하다. 이렇게 운동할 때, PB 의 길이 a에 대해 CQ의 길이 x를 “a의 로그”라 정의한다.

 

 

 

요즘에 배우는 로그와는 다르게 운동의 개념을 써서 기하학적으로 정의했음을 알 수 있는데, 이러고 보면 지난 시간에 설명한 오일러의 공식이 대수학, 기하학, 해석학에 관련된 공식이라는 것도 우연만은 아니다. 그런데 왜 로그를 사용하면 곱셈을 덧셈으로, 나눗셈을 뺄셈으로 바꿀 수 있다는 걸까? 네이피어는 초보적인 미분 개념이라 할 수 있는 운동의 1차 근사를 써서 설명했는데, 이 글에서는 조금 달리 설명하겠다.   네이피어의 로그를 LOG라 쓰기로 하면, 위의 그림에서 LOG(a)=x가 된다. 한편 Q는 항상 속도 1로 운동하므로, x는 Q까지 도달하는데 걸린 시간과 같다. 역으로 말하면, A를 출발한 점이 P에 도달하는데 걸린 시간이 LOG(a)일 때, PB의 길이가 a라는 얘기다. 이제 P에서 더 움직여 보자. 현재 속도는 PB의 길이 즉 a이다. 여기에서 LOG(b)만큼의 시간이 더 흐를 때 P가 도달하는 점 P’은 어디일까? PB와 AB 사이에 비례 관계를 잘 생각해보자. 원래 속도가 1인 상태에서 출발해서 LOG(a)만큼 시간이 흐르면 PB의 길이가 a가 된다고 하였다. 그러니 속도가 a인 상태에서 출발해서 LOG(b)만큼 시간이 흐르면 도착하는 점 P’와 B간의 거리는 a×b 즉 ab가 된다!

 

  

 

A를 출발한 점이 LOG(a) + LOG(b)만큼의 시간이 흐른 후 도달한 점이 P’이고 P’B의 길이가 ab이므로, 다음 관계를 얻는다.   b 대신 b/a를 대입하면, LOG(b) = LOG(a) + LOG(b/a)이므로 다음 식을 얻는다.     곱셈의 반복인 거듭제곱의 경우 LOG(an)=nLOG(a)임도 알 수 있다.     브리그스의 상용로그 네이피어의 발견은 격한 찬양을 받았다. 특히 헨리 브리그스(Henry Briggs, 1561-1631)는 런던을 떠나 에든버러까지 네이피어를 직접 찾아가, ‘이제는 누구나 쉽게 여기지만, 당신이 발견하기 전까지 아무도 발견하지 못했다는 것이 의아합니다’라며 존경을 바친다. 다음 해 한 번 더 찾아간 브리그스는 1에서의 로그값이 0이 되도록 로그의 정의를 조정하자는 의견을 내고 네이피어도 동의한다. 다만 네이피어는 병으로 인해 쇠약해 있어서, 새로운 로그표의 계산은 브리그스가 이어받게 된다. 브리그스는 시행착오를 거친 끝에 10에서의 로그값이 1이 되도록 하는 로그, 오늘날 상용로그 라 부르는 로그가, 10진법을 쓰는 인간에게 편리하다는 결론을 내린다. 브리그스는 1617년에는 1부터 1000까지의 로그값을 필두로, 10년 뒤에는 1부터 2만, 9만부터 10만까지의 자연수에 대해 상용로그값을 실은 로그표를 세상에 내놓는다. 이 로그표는 3세기 동안 가장 우수한 로그표의 자리를 내주지 않았다.     로그를 쓰면 계산이 쉬워진다 로그를 이용하면 어떻게 곱셈을 쉽게 할 수 있는지 상용로그를 써서 (log라고 쓰겠다) 예를 들어 보자. 상용로그일 때 log(10)=1로 정했으므로 log(10n) = nlog(10) = n이다. 여기에서는 예를 들어 250을 계산하기로 하자. 이를 위해 이 수의 로그값, 즉, log(250) = 50×log(2)을 계산한다. 로그표를 보면, log(2)=0.30102999…이므로, 다음과 같다.     한편 로그표를 거꾸로 뒤져보면, 0.0514998… = log(1.12589…)이므로 위의 식에 대입하여 다음을 알 수 있다.     로그표를 두 번 찾는 것만으로도 2의 50제곱을 상당히 정확하게 구할 수 있다. 당연한 얘기겠지만, 로그표가 정밀할수록 이 값은 더 정밀해진다.

 

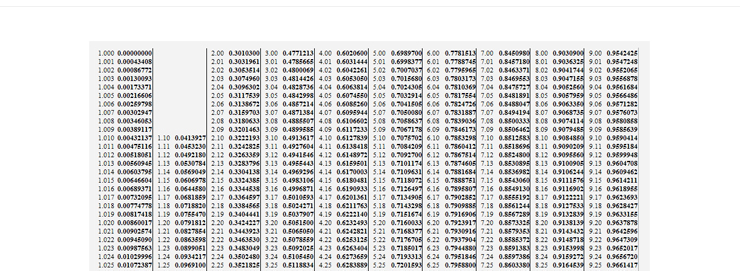
소수점 7자리까지 나온 상용로그표의 일부

 

 

 

천문학자의 수명을 두 배로 늘리다 티코 브라헤의 자료를 물려받아 천문학을 연구하던 요하네스 케플러(Johaness Kepler, 1571-1630)는 1609년 행성의 운동법칙 두 가지를 담은 ‘새 천문학’(Astronomial Nova)을 출간한다. 케플러의 회고에 따르면 세 번째 법칙인 ‘행성의 공전주기는 태양과의 평균 거리의 1.5제곱’이라는 법칙은 1618년 ‘마음을 폭풍처럼 뒤흔든 새로운 전략’을 택해 얻어냈다고 한다. 케플러가 택한 전략이 무엇이었는지는 정확히 알려져 있지는 않다. 다만, 케플러가 독자적으로 로그표를 만들었으며 로그의 보급에 앞장선 것으로 미루어보아, 공전주기와 평균 거리의 로그값을 구해 비교한 결과, 그 값이 1.5배라는 것을 발견했을 것으로 짐작한다.

 

 

이와 같이 천문학에 끼친 영향을 두고 라플라스는 ‘로그의 발견으로 천문학자의 수명이 두 배가 되었다’고 평하기도 하였다. 그러나, 케플러의 운동법칙의 발견이 곧이어 뉴턴의 발견으로 이어진다는 점 등을 미루어볼 때, 로그의 발견이 천문학뿐만 아니라 수학에 있어서도 획기적인 사건이었다는 데 이의를 달 수는 없을 것이다.

  

 

1. 로그(logarithm)

   a가 1이 아닌 양수일 때 x=a^y라면, y를 a를 밑으로 하는 x의 로그라고 하며, y=log_ax라고 쓴다. 로그는 네이피어가 창안한 것인데, 그는 지수와 무관하게 로그를 발견했다. 로그와 지수의 관련성의 발견은 후대의 일이다.

2. 상용로그(common logarithm)

   브리그스가 로그 발견자 네이피어의 조언을 구해 창안한 것으로 10을 밑으로 한 로그이다. 이를 이용하면 계산이 획기적으로 쉬워진다. 일반적으로 log x의 형태로 밑을 생략하고 쓴다.

 

 

 

글 정경훈 / 서울대 기초교육원 강의교수

서울대학교 수학과에서 학사, 석사, 박사를 받고, 포항공대, 연세대, 위스콘신대, 서울대에서 박사후 과정을 밟았다. 현재 서울대 기초교육원 강의교수이다.

 

 출처 : http://navercast.naver.com/science/math/2630